We argue for the value of small- to mid-scale environments in deep RL for increasing scientific insight and help make our community more inclusive.

Johan S. Obando-Ceron and Pablo Samuel Castro

This is a summary of our paper which was accepted at the Thirty-eighth International Conference on Machine Learning (ICML'21). (An initial version was presented at the deep reinforcement learning workshop at NeurIPS 2020).

The code is available here.

You can see the Deep RL talk here.

Introduction

Since the introduction of DQN (Mnih et al., 2015) reinforcement learning has witnessed a dramatic increase in research papers (Henderson et al., 2018). A large portion of these papers propose new methods that build on the original DQN algorithm and network architecture, often adapting methods introduced before DQN to work well with deep networks. New methods are typically evaluated on a set of environments that have now become standard, such as the Arcade Learning Environment (ALE) (Bellemare et al., 2012) and the control tasks available in MuJoCo and DM control suites (Todorov et al., 2012), (Tassa et al., 2020).

While these benchmarks have helped to evaluate new methods in a standardized manner, they have also implicitly established a minimum amount of computing power in order to be recognized as valid scientific contributions.

Furthermore, at a time when efforts such as Black in AI and LatinX in AI are helping bring people from underrepresented (and typically underprivileged) segments of society into the research community, these newcomers are faced with enormous computational hurdles to overcome if they wish to be an integral part of said community.

In this work we argue for a need to change the status-quo in evaluating and proposing new research to avoid exacerbating the barriers to entry for newcomers from underprivileged communities.

We complement this argument by revisiting the Rainbow algorithm (Hessel et al., 2018), which proposed a new state of the art algorithm by combining a number of recent advances, on a set of small- and medium-sized tasks. This allows us to conduct a “counterfactual” analysis: would Hessel et al. [2018] have reached the same conclusions if they had run on the smaller-scale experiments we investigate here? We extend this analysis by investigating the interaction between the different algorithms considered and the network architecture used; this is an element not explored by Hessel et al. [2018], yet as we show below, is crucial for proper evaluation of the methods under consideration.

This blog post is structured as follows:

• We first present a rough estimate of the computational and economic cost of rainbow, highlighting how these types of papers could only come from large research groups.
• In Revisiting Rainbow we revisit the original Rainbow experiments using a set of small- and mid-scale environments. We investigate whether the same conclusions would have been reached as in the original paper, but with a reduced computational expense.
• In Beyond the Rainbow we leverage the low computational cost of our chosen environment suites and perform an investigation into network architectures and batch sizes, distribution parameterizations, Munchausen RL, and reevaluating the Huber loss.
• We compare all our different Rainbow variants in rainbow flavours.
• Finally, we present some concluding remarks.

The Cost of Rainbow

Although the value of the Rainbow agent is undeniable, this result could have only come from a large research laboratory with ample access to compute:

• It takes roughly 5 days to train an Atari game on a Tesla P100 GPU
• There are 57 games in total
• To report performance with confidence bounds it is common to use at least five independent runs

Thus, to provide the convincing empirical evidence for Rainbow, Hessel et al. [2018] required at least 34,200 GPU hours (or 1425 days); in other words, these experiments must be run in parallel with multiple GPUs.

Considering that the cost of a Tesla P100 is about US$6,000, it becomes prohibitively expensive for smaller research laboratories. To put things in perspective, the average minimum monthly wage in Latin America (excluding Venezuela) is approximately US$313 (data taken from here); in other words, one GPU is the equivalent of approximately 20 minimum wages. Needless to say, this is far from inclusive.

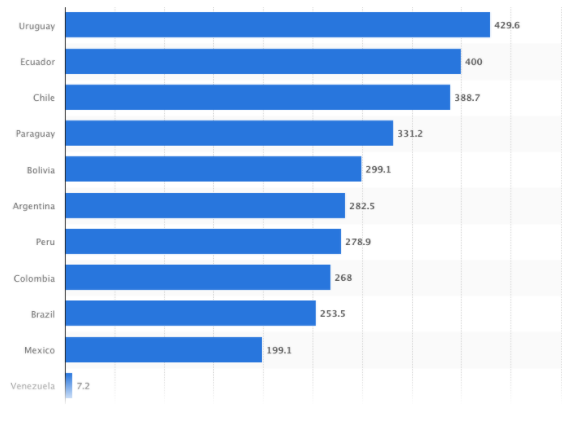
In light of this, we wish to investigate three questions:

1. Would Hessel et al. (2018) have arrived at the same qualitative conclusions, had they run their experiments on a set of smaller-scale experiments?
2. Do the results of Hessel et al. (2018) generalize well to non-ALE environments, or are their results overlyspecific to the chosen benchmark?
3. Is there scientific value in conducting empirical research in reinforcement learning when restricting oneself to small- to mid-scale environments?

We investigate the first two in the next section, and the last in Beyond the Rainbow.

Revisiting Rainbow

As in the original Rainbow paper, we evaluate the effect of adding the following components to the original DQN algorithm:

• Double Q-learning mitigates overestimation bias in the Q-estimates by decoupling the maximization of the action from its selection in the target bootstrap.
• Prioritized experience replay samples trajectories from the replay buffer proportional to their respective temporal difference error.
• Dueling networks uses two streams sharing the initial convolutional layers, separately estimating $V^*(s)$ and the advantages for each action
• Multi-step learning uses multi-step targets for temporal difference learning
• Distributional RL maintains estimates of return distributions, rather than return values.
• Noisy Nets replaces standard $\epsilon$-greedy exploration with noisy linear layers that include a noisy stream.

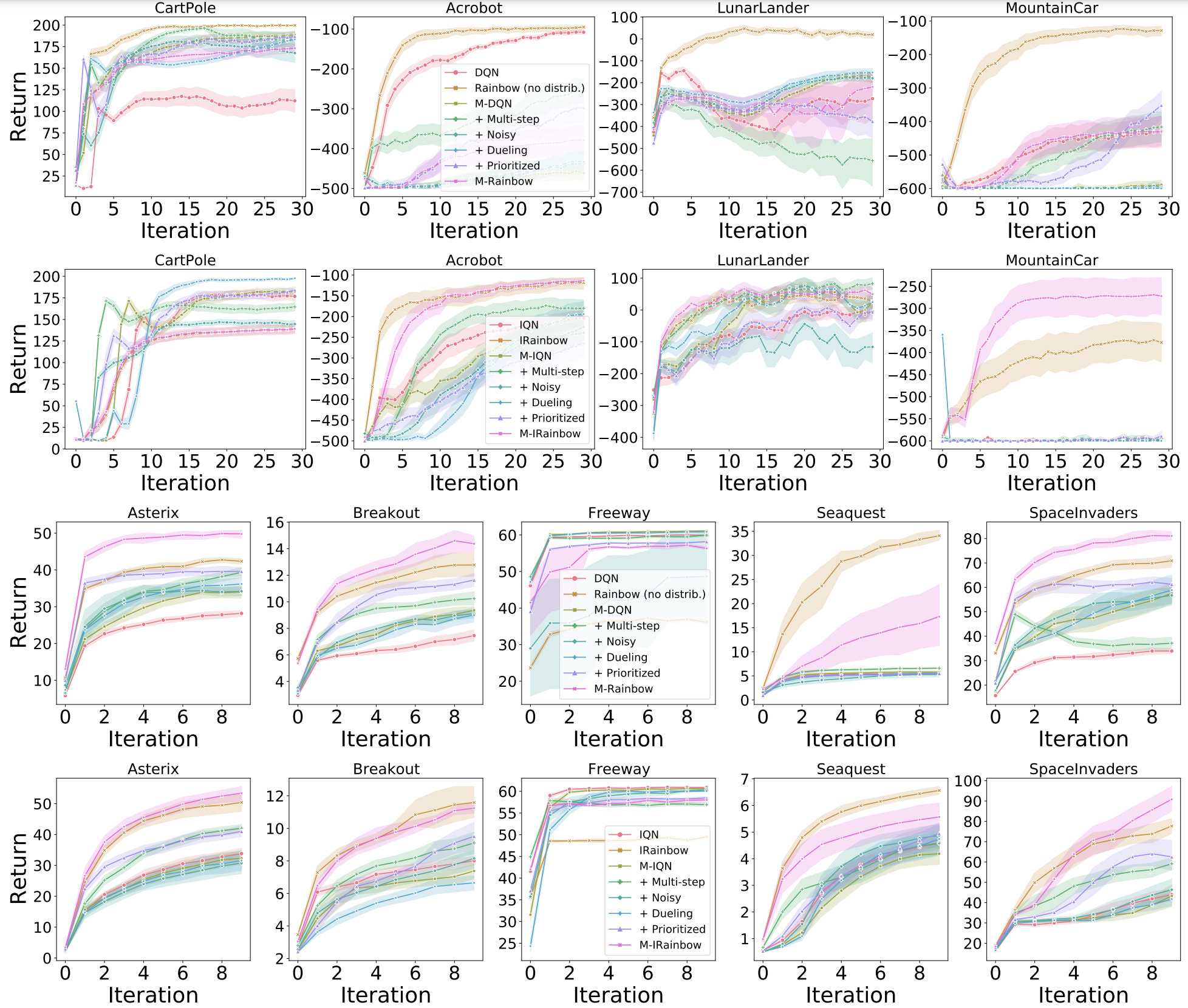
Classic control

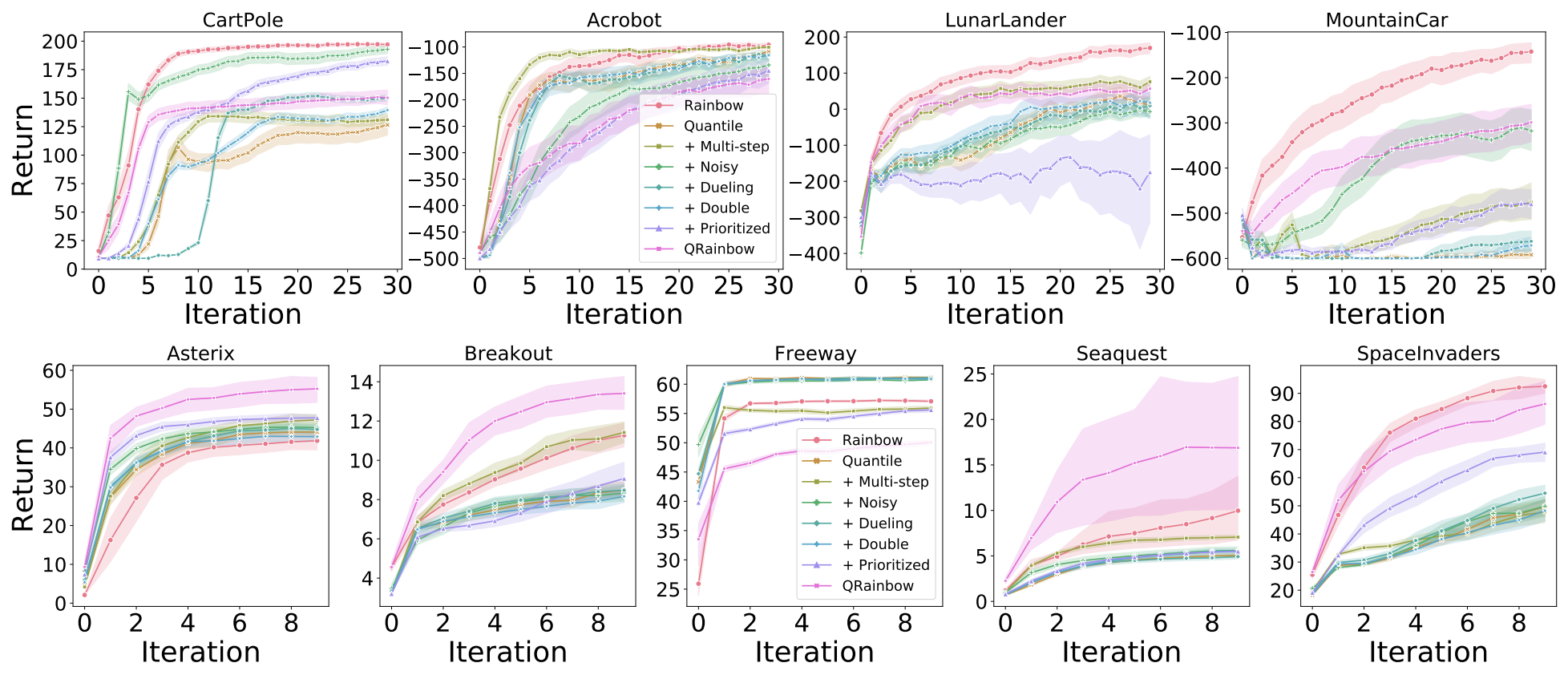
Our first set of experiments were performed on four classic control environments: CartPole, Acrobot, LunarLander, and MountainCar. We first investigate the effect of independently adding each algorithmic component to DQN (top row):

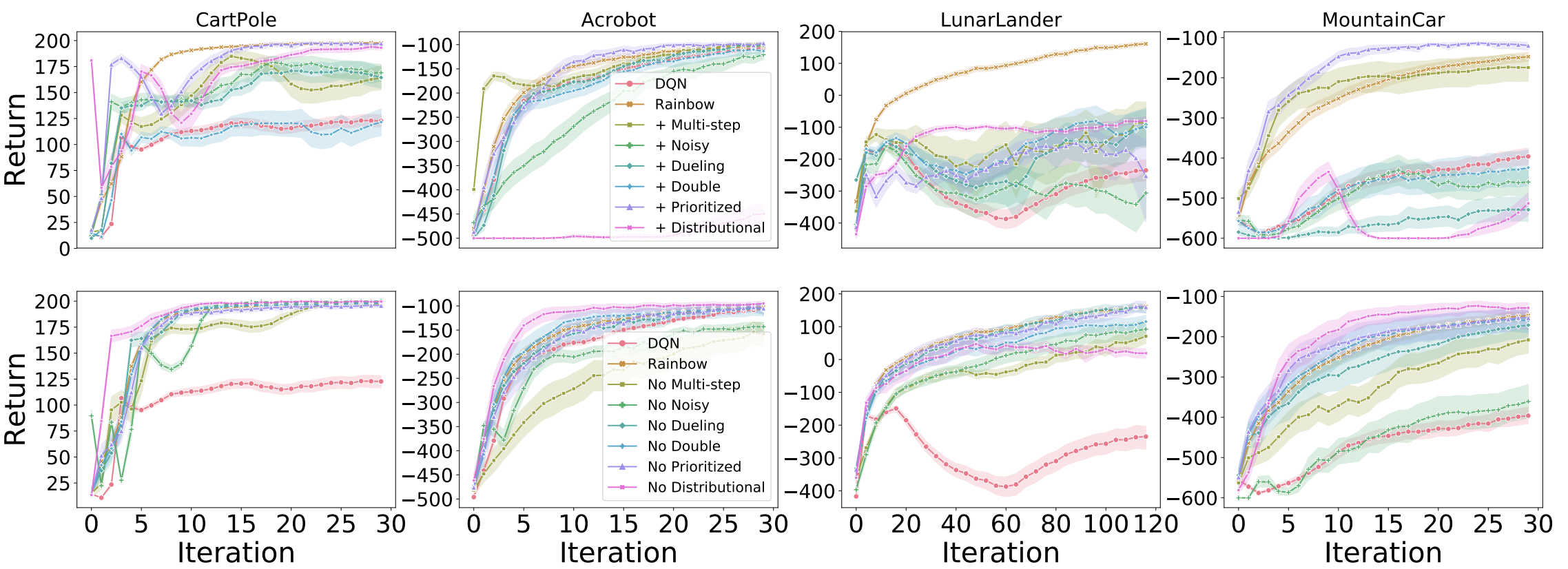
Just like Hessel et al. [2018] we find that, in aggregate, the addition of each of these algorithms does improve learning over the base DQN. However, while Hessel et al. [2018] found prioritized replay and multi-step to be the most impactful additions, in these environments the gains from these additions are more tempered. What is most interesting is that when distributional RL is added to DQN without any of the other components, the gains can sometimes be minimal (see LunarLander), and can sometimes have a large negative effect on learning (Acrobot and MountainCar). This is consistent across the various learning rates we considered.

In contrast, when we look at the removal of each of these components from the full Rainbow agent (bottom row in above figure), we can see that what hurts the most is the removal of distributional RL. These results suggest there is a symbiotic between distributional RL and one of the other algorithms considered, an investigation that warrants investigation in future work, along the lines of the theoretical investigation by Lyle et al. [2019], which demonstrated that the combination of distributional RL with non-linear function approximators can sometimes have adverse effects on training.

MinAtar

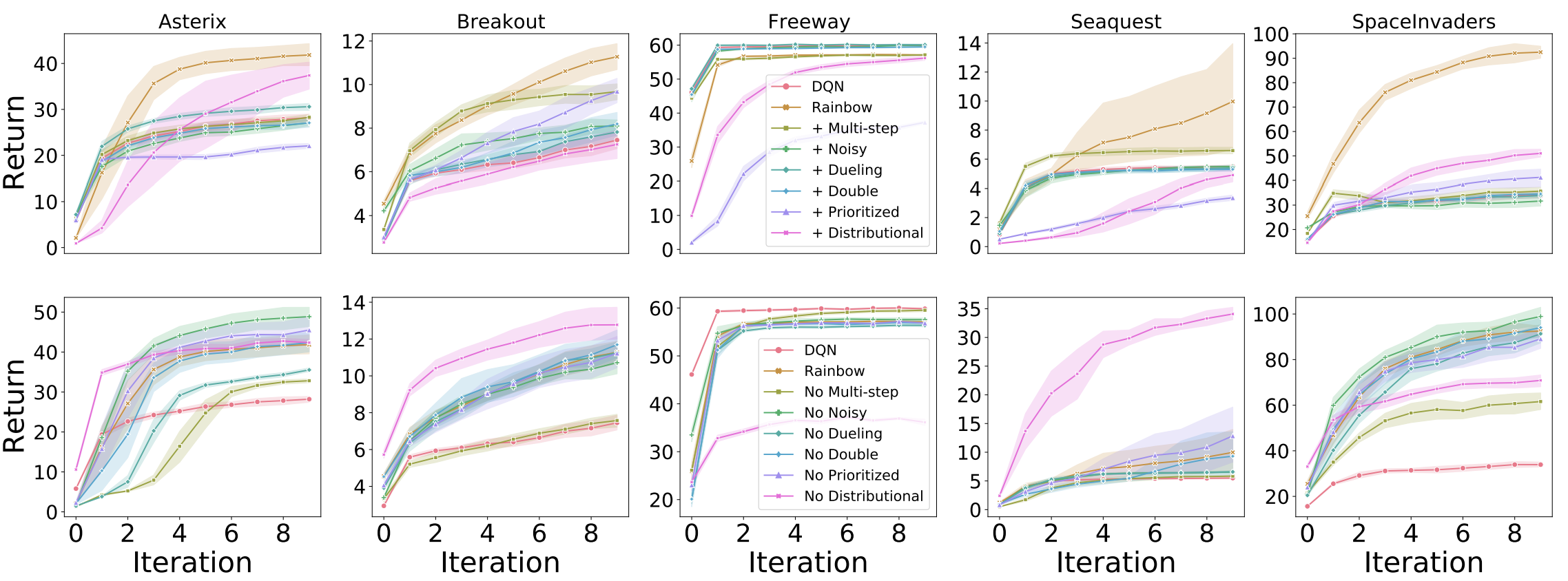
In order to strengthen the Rainbow connection, we also ran a set of experiments on the MinAtar environment Young and Tian, 2019, which is a set of miniaturized versions of five ALE games (Asterix, Breakout, Freeway, Seaquest, and SpaceInvaders). These environments are considerably larger than the four classic control environments previously explored, but they are significantly faster to train than regular ALE environments. Specifically, training one of these agents takes approximately 12-14 hours on a P100 GPU. For these experiments, we followed the network architecture used by Young and Tian [2019] consisting of a single convolutional layer followed by a linear layer.

In these experiments we still find distributional RL to be the most significant of the additions, but it does not seem to require being coupled with another algorithm to produce improvements. This begs the question as to whether the use of distributional RL with convolutional layers avoids the pitfalls sometimes observed in the classic control experiments. However, the results from Seaquest suggest that the combination with one of the algorithms is hurting performance; based on the ablation results from Rainbow, it appears that noisy networks have a detrimental effect on performance.

Conclusions

When viewed in aggregate we find our results consistent with those of Hessel et al., 2018: the results for each algorithmic component can vary from environment to environment. If we were to suggest a single agent that balances the tradeoffs of the different algorithmic components, our version of Rainbow would likely be consistent with Hessel et al.: combining all components produces a better overall agent.

However, there are important details in the variations of the different algorithmic components that merit a more thorough investigation. An important finding of our work is that distributional RL, when added on its own to DQN, may actually hurt performance. Our investigation suggests that its true benefits come when combined with another algorithmic component (in the classic control environments) or when used on a convolutional neural network (as in the MinAtar games). Investigating these interactions further will lead to a better understanding of distributional RL.

Beyond the Rainbow

We leverage the low cost of the small-scale environments to conduct a more thorough investigation into some of the algorithmic components studied above.

Network architectures & batch sizes

We investigated the interaction of the best per-game hyperparameters with the number of layers and units per layer.

The plot below presents the results for DQN:

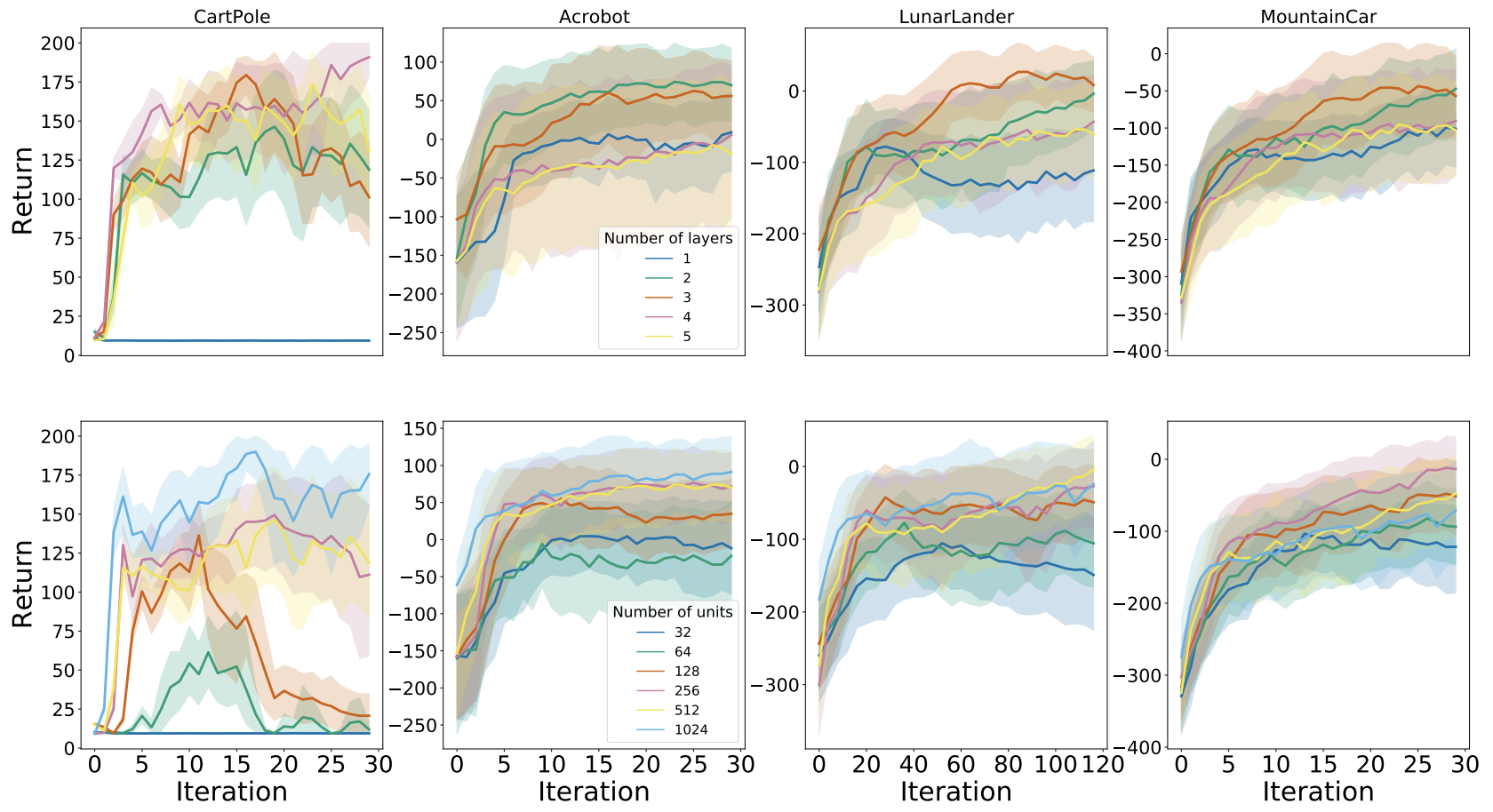
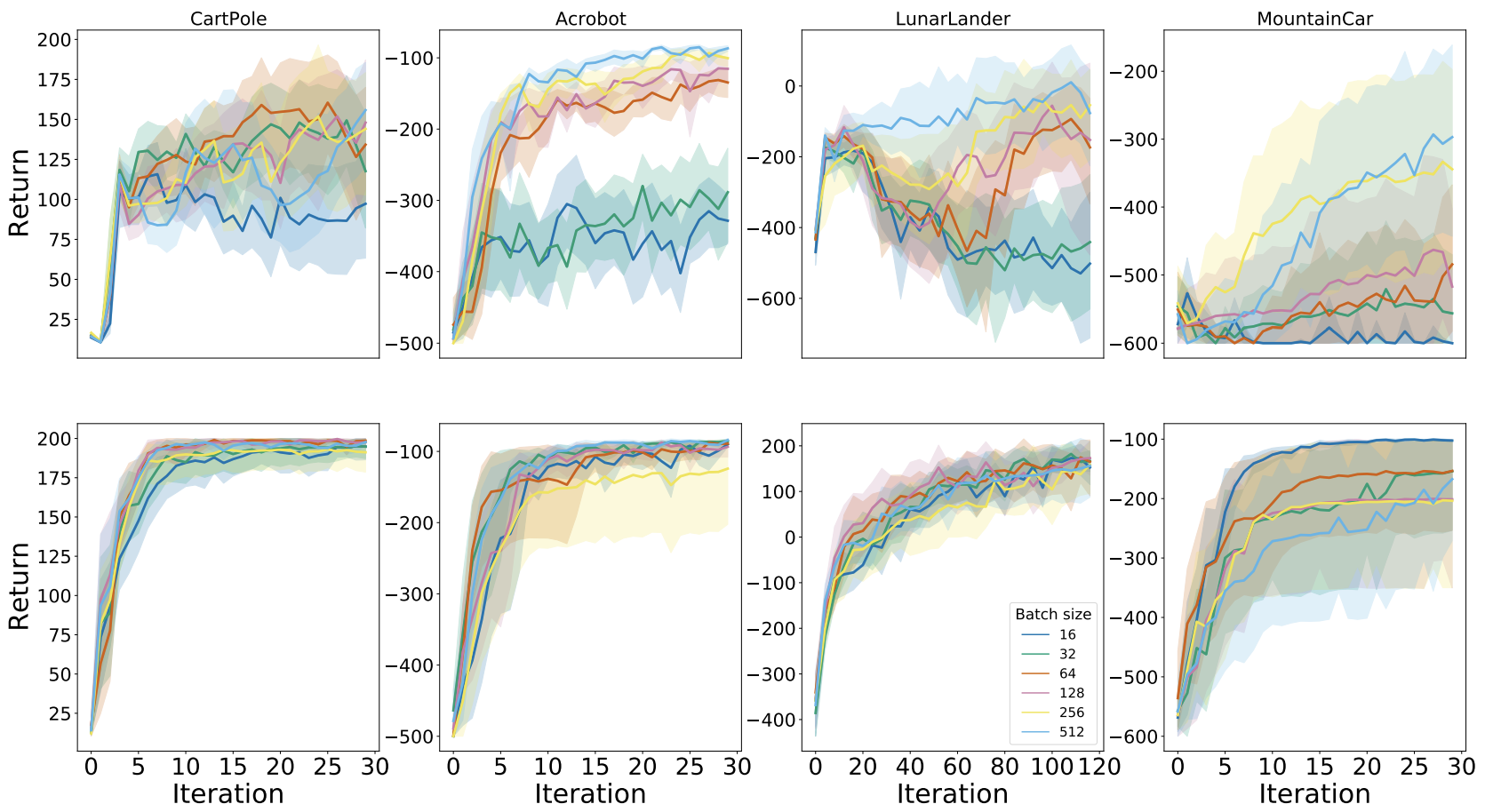
And the following plot displays the results for Rainbow:

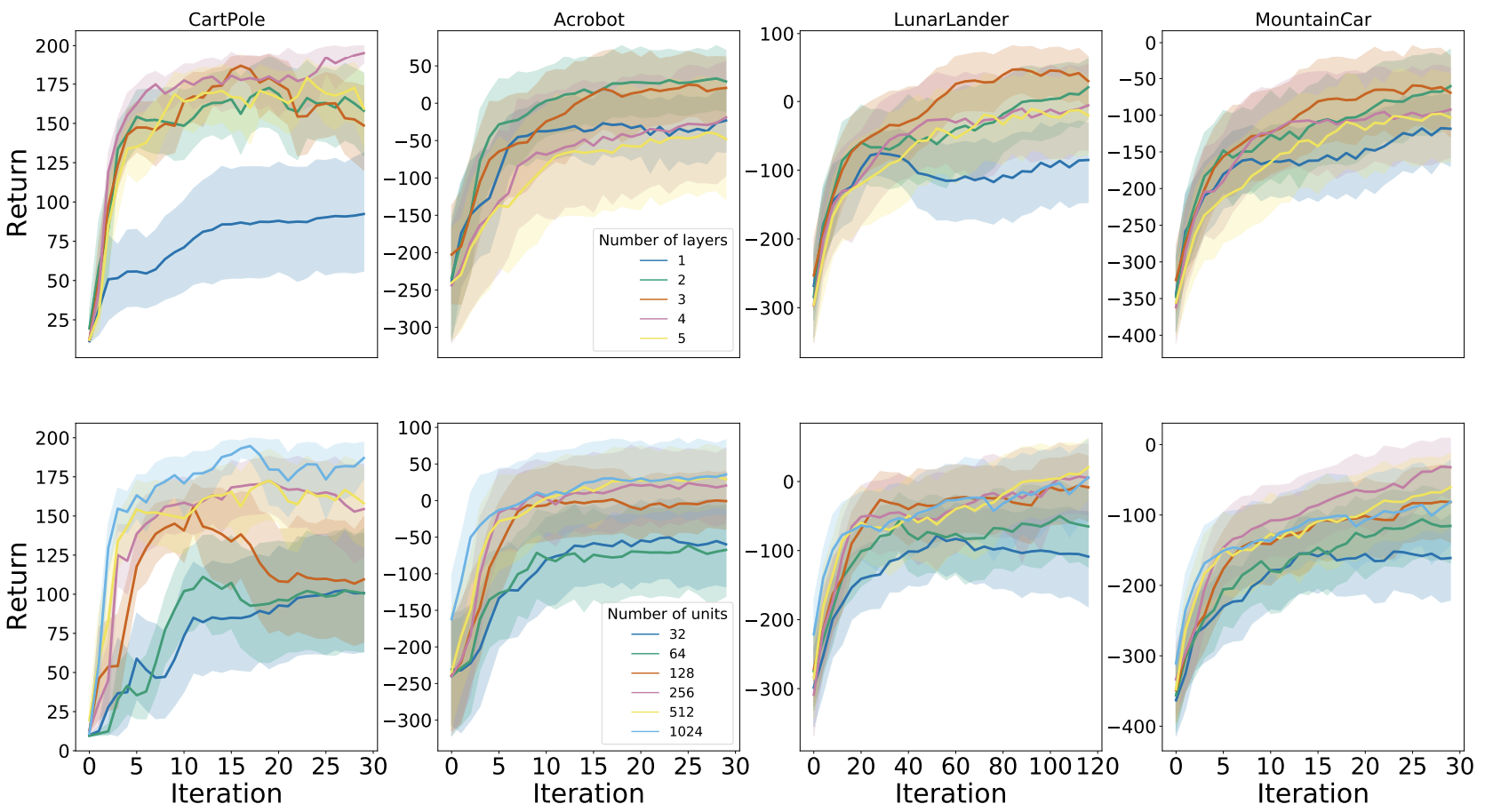
We found that in general using 2-3 layers with at least 256 units each yielded the best performance. Further, aside from Cartpole, the algorithms were generally robust to varying network architecture dimensions.

Another often overlooked hyper-parameter in training RL agents is the batch size. We investigated the sensitivity of DQN (top) and Rainbow (bottom) to varying batch sizes and found that while for DQN it is sub-optimal to use a batch size below 64, Rainbow seems fairly robust to both small and large batch sizes.

Distribution parameterizations

Although distributional RL is an important component of the Rainbow agent, at the time of its development Rainbow was only evaluated with the C51 parameterization of the distribution, as originally proposed by Bellemare et al. (2017). Since then there have been a few new proposals for parameterizing the return distribution, notably quantile regression and implicit quantile networks (IQN).

We evaluated modified versions of the Rainbow agent, where the distribution is parameterized using either QR-DQN or IQN.

QR-DQN

In the figure below, we evaluate the interaction of the different Rainbow components with Quantile and find that, in general, QR-DQN responds favourably when augmented with each of the components. We also evaluate a new agent, QRainbow, which is the same as Rainbow but with the QR-DQN parameterization. It is interesting to observe that in the classic control environments Rainbow outperforms QRainbow, but QRainbow tends to perform better than Rainbow on Minatar (with the notable exception of Freeway), suggesting that perhaps the quantile parameterization of the return distribution has greater benefits when used with networks that include convolutional layers.

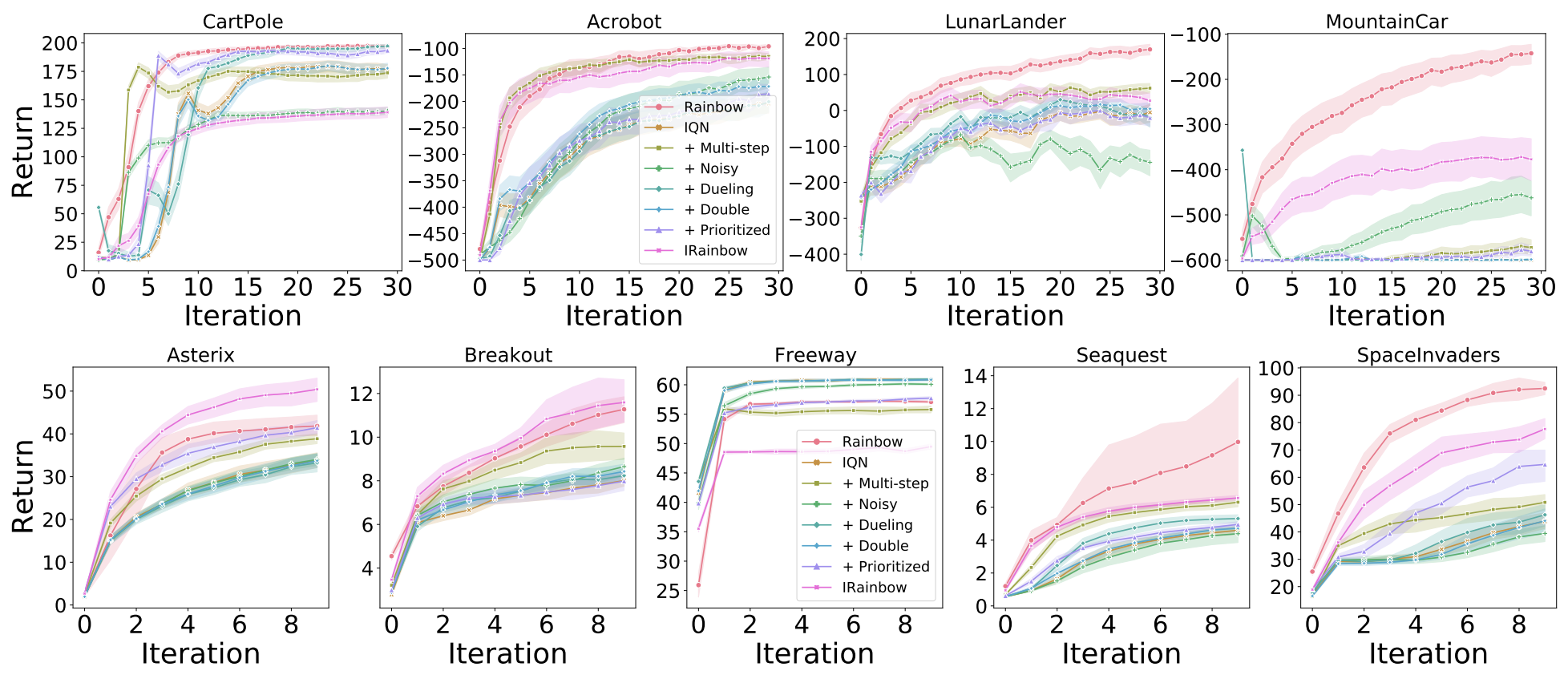
IQN

In contrast to QR-DQN, in the classic control environments the effect on performance of various Rainbow components is rather mixed and, as with QR-DQN IRainbow underperforms Rainbow. In Minatar we observe a similar trend as with QR-DQN: IRainbow outperforms Rainbow on all the games except Freeway.

Munchausen RL

Vieillard et al. (2020) introduced Munchausen RL as a simple variant to any temporal difference learning agent consisting of two main components: the use of stochastic policies and augmenting the reward with the scaled logpolicy. Integrating their proposal to DQN yields M-DQN with performance superior to that of C51; the integration of Munchausen-RL to IQN produced M-IQN, a new state-ofthe art agent on the ALE.

In the figure below we report the results when repeating the Rainbow experiment on M-DQN and M-IQN. In the classic control environments neither of the Munchausen variants seem to yield much of an improvement over their base agents. In Minatar, while M-DQN does seem to improve over DQN, the same cannot be said of M-IQN. We explored combining all the Rainbow components with the Munchausen agents and found that, in the classic control environments, while M-Rainbow underperforms relative to its non-Munchausen counterpart, M-IRainbow can provide gains. In Minatar, the results vary from game to game, but it appears that the Munchausen agents yield an advantage on the same games (Asterix, Breakout, and SpaceInvaders).

Reevaluating the Huber loss

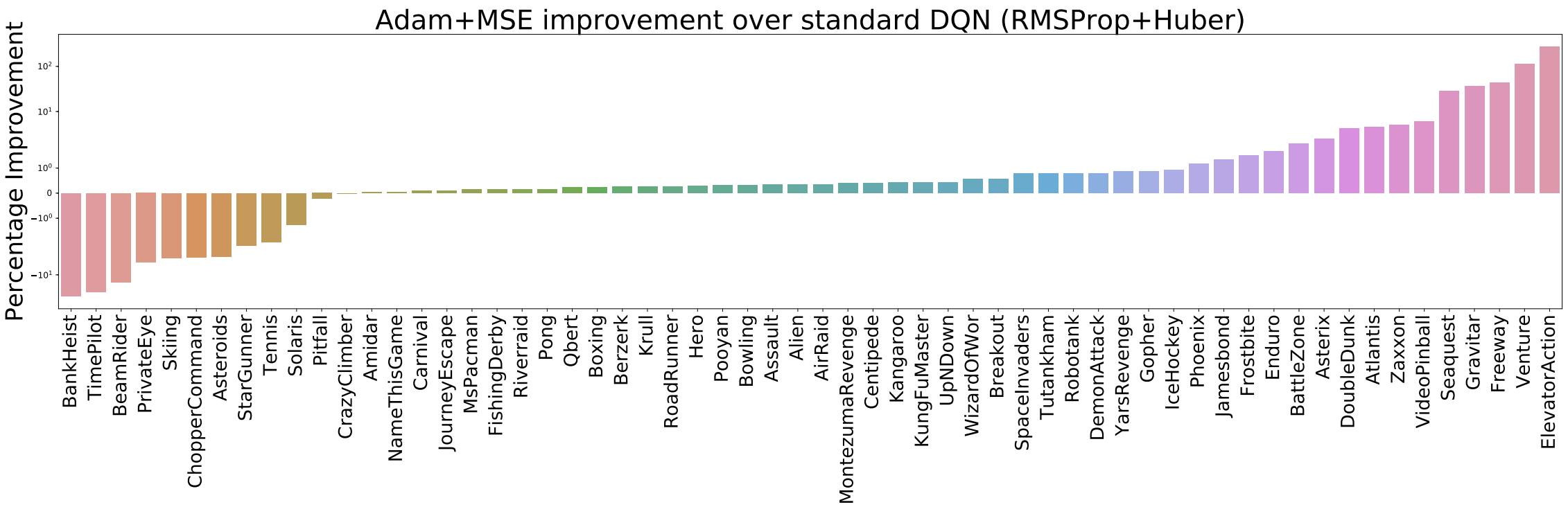
The Huber loss is what is usually used to train DQN agents as it is meant to be less sensitive to outliers. Based on recent anecdotal evidence, we decided to evaluate training DQN using the mean-squared error (MSE) loss and found the surprising result that on all environments considered using the MSE loss yielded much better results than using the Huber loss, sometimes even surpassing the performance of the full Rainbow agent (full classic control and Minatar results are provided in the appendix). This begs the question as to whether the Huber loss is truly the best loss to use for DQN, especially considering that reward clipping is typically used for most ALE experiments, mitigating the occurence of outlier observations. Given that we used Adam for all our experiments while the original DQN algorithm used RMSProp, it is important to consider the choice of optimizer in answering this question.

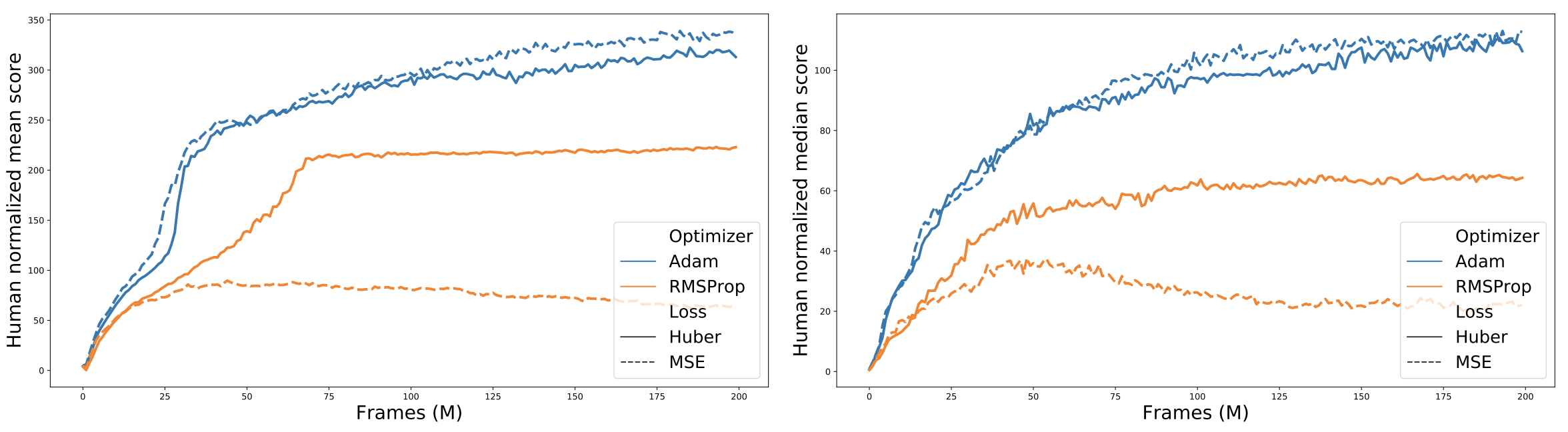
To obtain an answer, we compared the performance of the Huber versus the MSE loss when used with both the Adam and RMSProp optimizers on all 60 Atari 2600 games. We find that, overwhelmingly, Adam+MSE is a superior combination than RMSProp+Huber.

Additionally, when comparing the various optimizer-loss combinations we find that, when using RMSProp, the Huber loss tends to perform betterthan MSE, which in retrospect explains why Mnih et al. chose the Huber over the simpler MSE loss when introducing DQN.

Our findings highlight the importance in properly evaluating the interaction of the various components used when training RL agents, as was also argued by Fujimoto et al. (2020) with regards to loss functions and non-uniform sampling from the replay buffer; as well as by Hessel et al. (2019) with regards to inductive biases used in training RL agents.

Finally, we note that the Dopamine baseline plots now contain DQN with Adam and MSE as one of the included baselines.

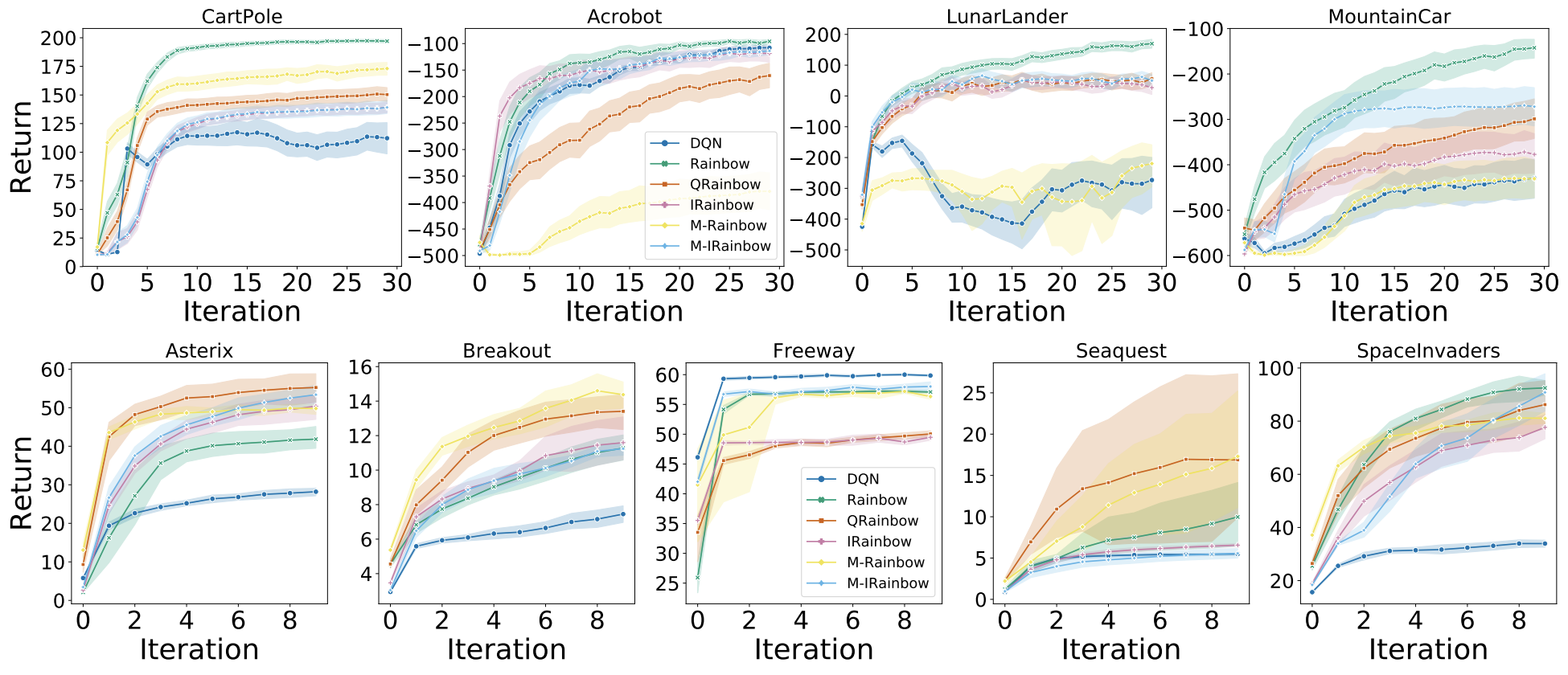
Rainbow flavours

We compare the performance of DQN against all of the Rainbow variants and show the results below. This figure highlight the fact that, although Rainbow does outperform DQN, there are important differences amongst the various flavours that invite further investigation.

Conclusion

On a limited computational budget we were able to reproduce, at a high-level, the findings of Hessel et al. [2018] and uncover new and interesting phenomena. Evidently it is much easier to revisit something than to discover it in the first place. However, our intent with this work was to argue for the relevance and significance of empirical research on small- and medium-scale environments. We believe that these less computationally intensive environments lend themselves well to a more critical and thorough analysis of the performance, behaviours, and intricacies of new algorithms.

It is worth remarking that when we initially ran 10 independent trials for the classic control environments, the confidence intervals were very wide and inconclusive; boosting the independent trials to 100 gave us tighter confidence intervals with small amounts of extra compute. This would be impractical for most large-scale environments.

We are by no means calling for less emphasis to be placed on large-scale benchmarks. We are simply urging researchers to consider smaller-scale environments as a valuable tool in their investigations, and reviewers to avoid dismissing empirical work that focuses on these smaller problems. By doing so, we believe, we will get both a clearer picture of the research landscape and will reduce the barriers for newcomers from diverse, and often underprivileged, communities. These two points can only help make our community and our scientific advances stronger.

Acknowledgements

The authors would like to thank Marlos C. Machado, Sara Hooker, Matthieu Geist, Nino Vieillard, Hado van Hasselt, Eleni Triantafillou, and Brian Tanner for their insightful comments on our work.