Contrastive Behavioral Similarity Embeddings for Generalization in Reinforcement Learning

This paper was accepted as a spotlight at ICLR'21.

We propose a new metric and contrastive loss that comes equipped with theoretical and empirical results.

Policy Similarity Metric

We introduce the policy similarity metric (PSM) which is based on bisimulation metrics. In contrast to bisimulation metrics (which is built on reward differences), PSMs are built on differences in optimal policies.

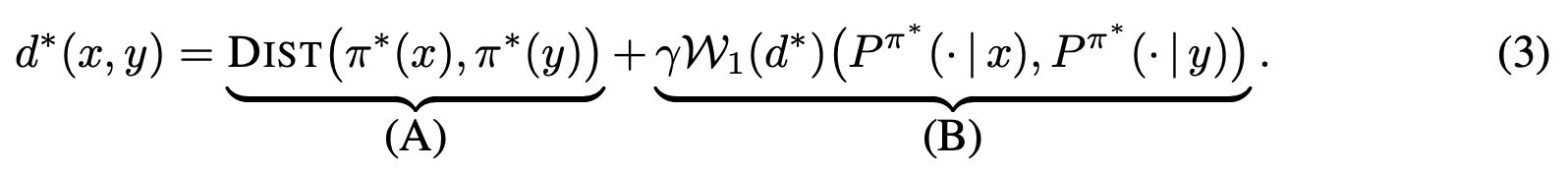
If we were to use this metric for policy transfer (as Doina Precup & I explored previously), we can upper-bound the difference between the optimal and the transferred policy:

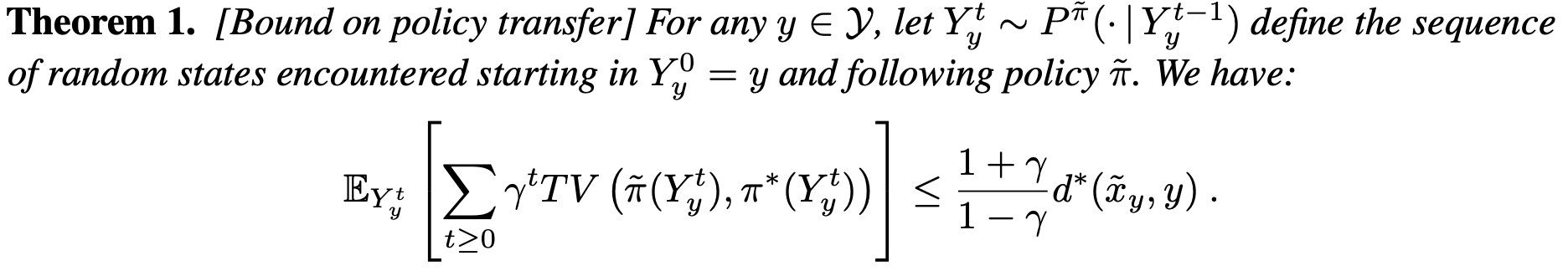
Policy Similarity Embeddings

We use this metric to define a loss for learning contrastive metric embeddings (CMEs) that aim to learn a structured representation respecting $d^*$.

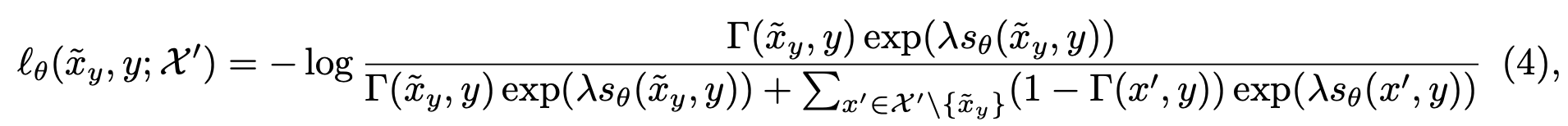
The resulting algorithm is as follows:

Empirical Evaluations

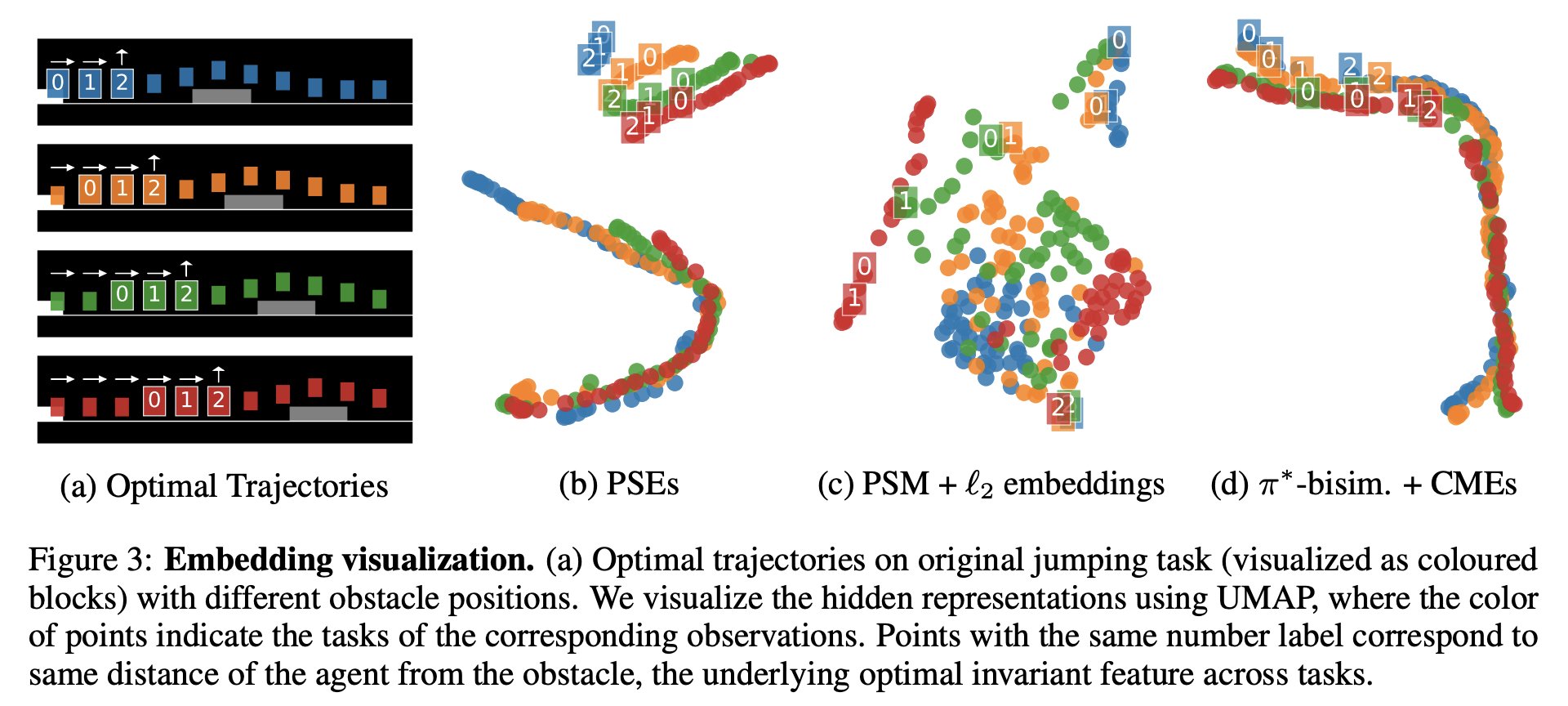
Jumping Task

We first evaluate this loss on the jumping task which, although seemingly simple, proves surprisingly hard to generalize in. our method produces the overall best results, both in quantitative terms:

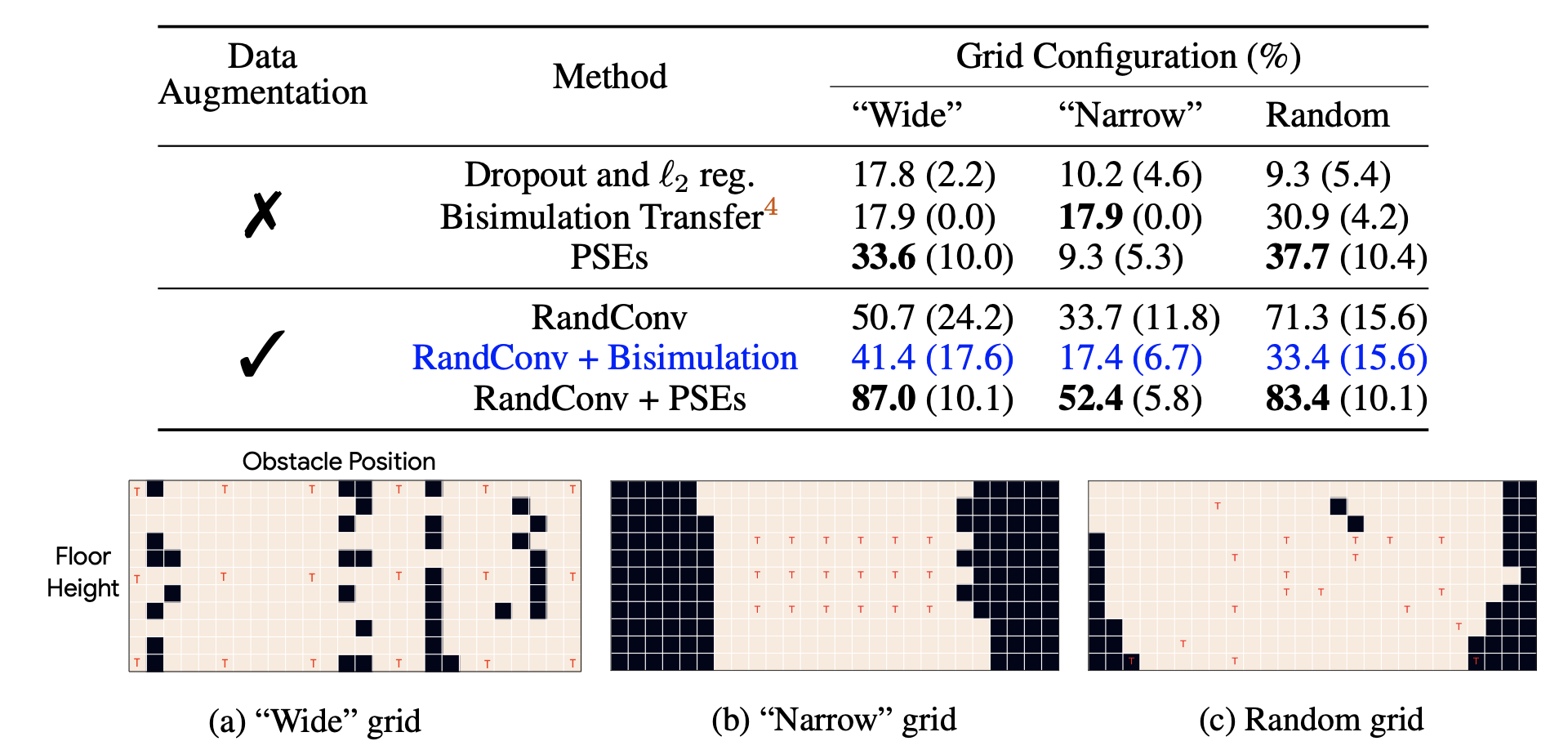
As well as in qualitative terms:

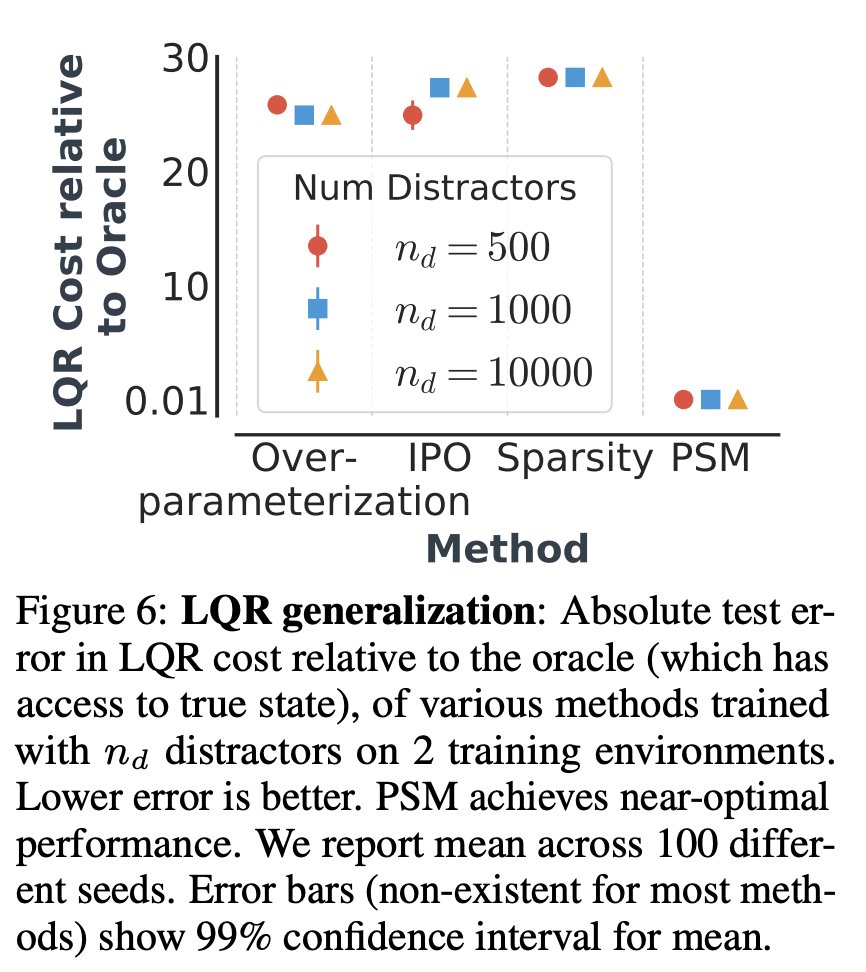
Linear Quadratic Regulators with spurious correlations

We also evaluated on a linear quadratic regulator with distractors where we obtained really great performance:

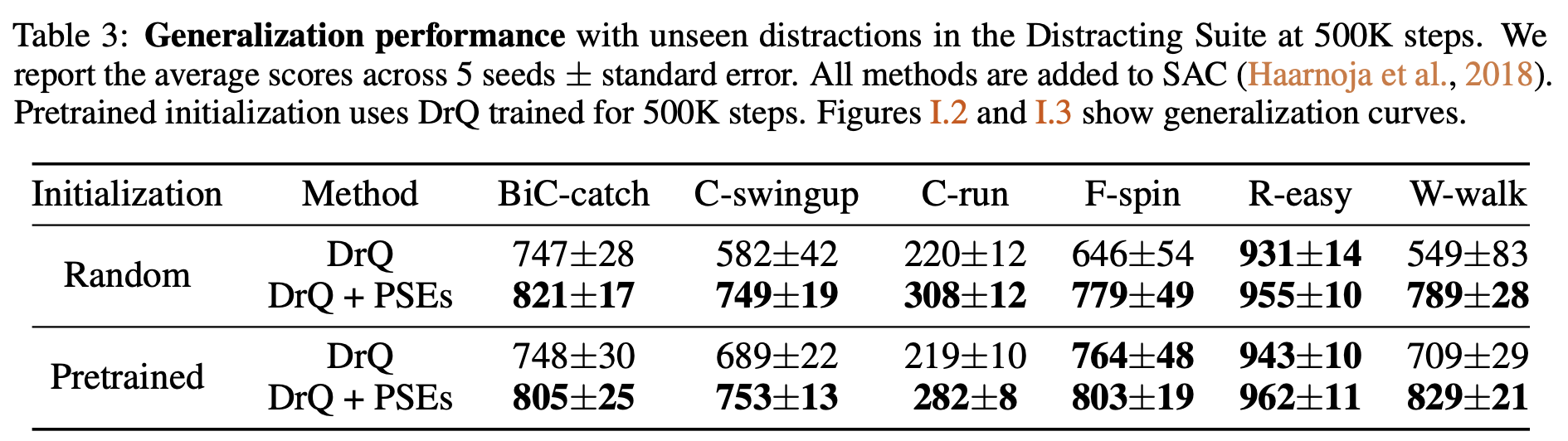
DM-Control suite

Finally, we also evaluated on the recently-released distracting control suite where we augment the current SOTA with an auxiliary loss for learning PSEs. This produced a new SOTA :)