Metrics and continuity in reinforcement learning

In this work we investigate the notion of “state similarity” in Markov decision processes. This concept is central to generalization in RL with function approximation.

Our paper was published at AAAI'21.

Charline Le Lan, Marc G. Bellemare, and Pablo Samuel Castro

The text below was adapted from Charline’s twitter thread

In RL, we often deal with systems with large state spaces. We can’t exactly represent the value of each of these states and need some type of generalization. One way to do that is to look at structured representations in which similar states are assigned similar predictions.

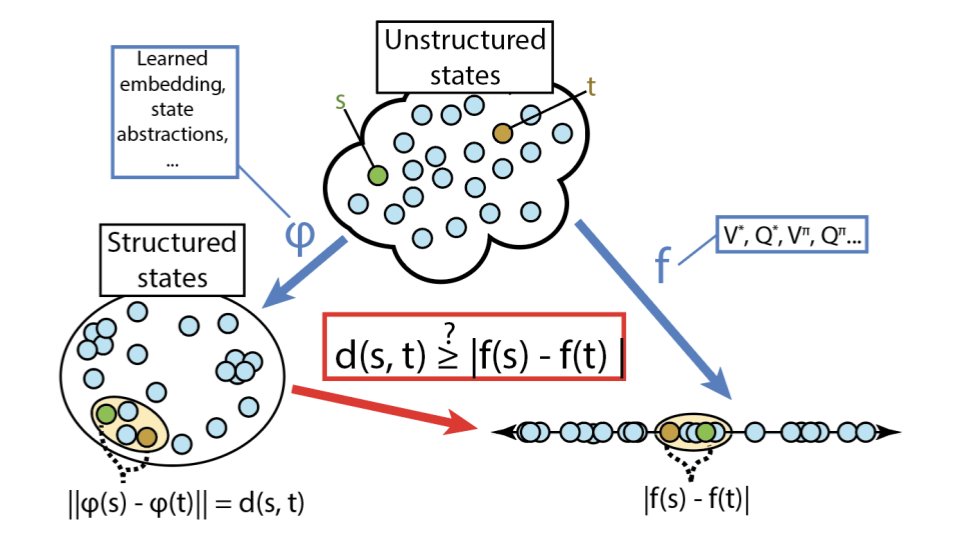
We consider the case where these representations are induced by state metrics. How shall we choose a metric to get good generalization properties? An interesting metric should give us continuity properties for the RL function of interest in our problem. A good metric should also give us a representation as coarse as possible so that we can cheaply generalize to new states.

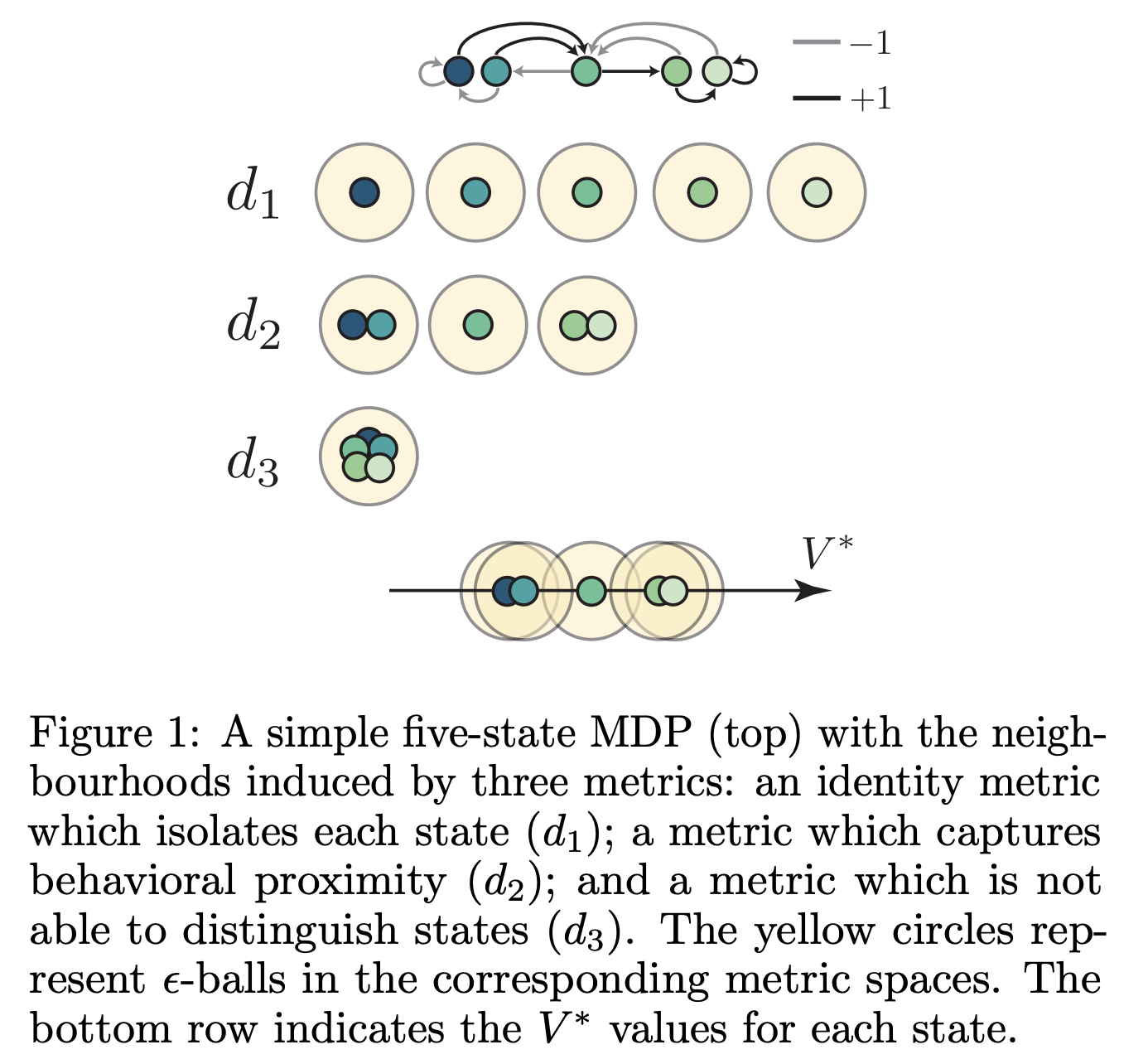
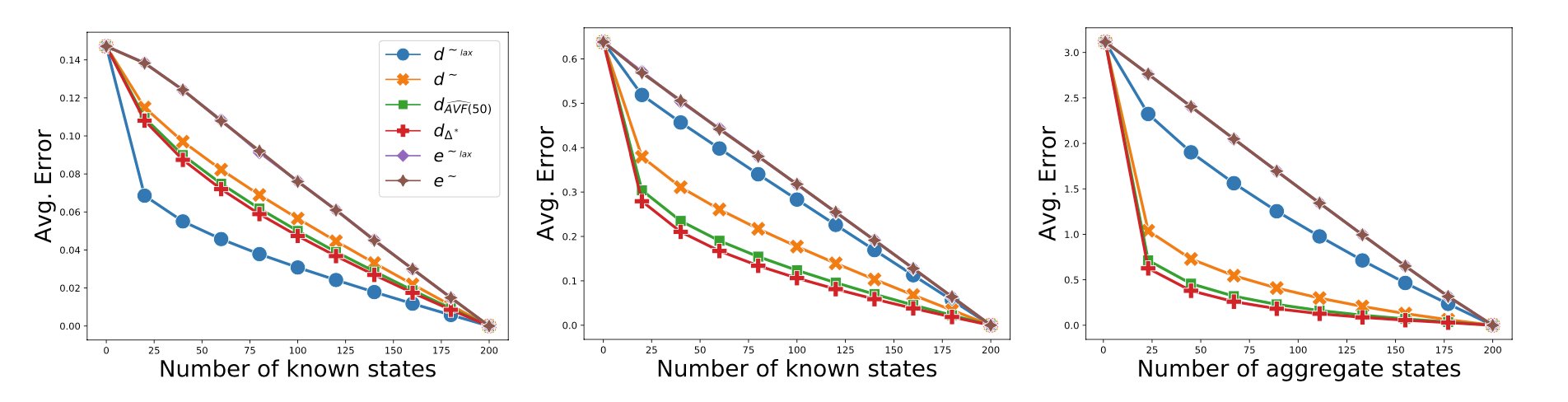
Having these state similarity metrics allow us to define “neighbourhoods”: all states that are within at most $\epsilon$ apart. This allows us, for instance, to transfer things such as value functions through a state’s neighbourhood.

Our paper unifies representations of states spaces and the notion of continuity via a taxonomy of metrics. We also provide a hierarchy of metrics to compare the topologies induced by all these metrics.

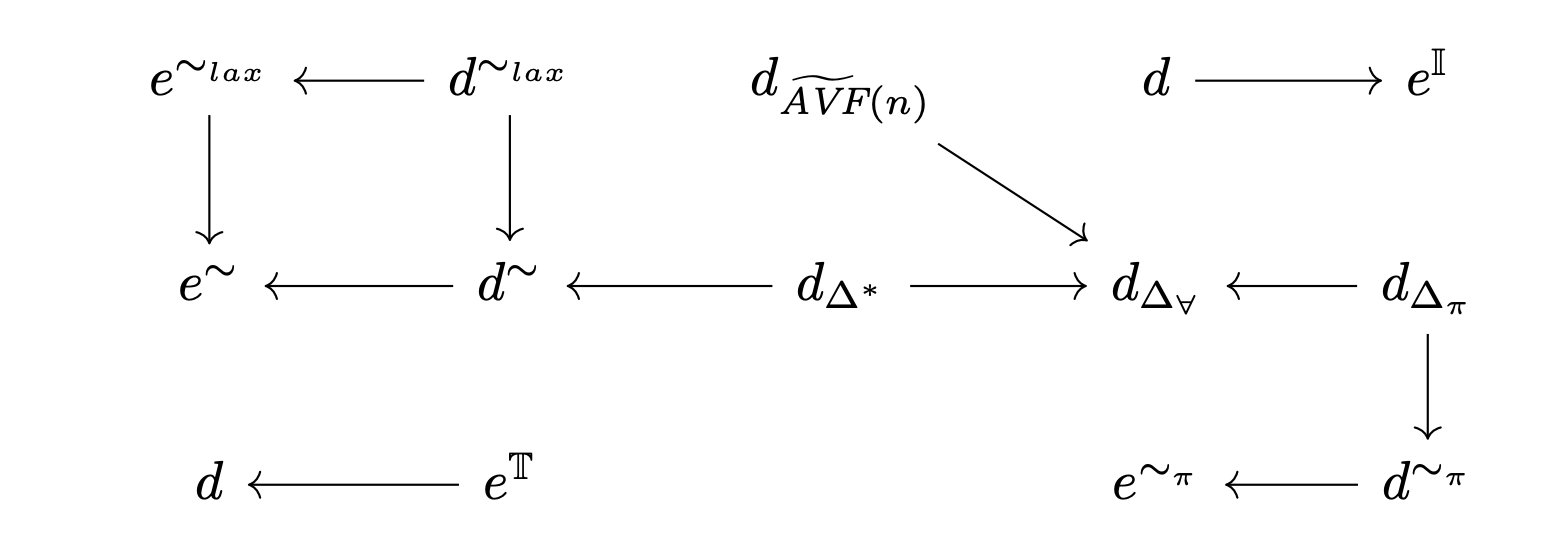
Using our taxonomy, we find that most commonly discussed metrics are actually poorly suited for algorithms that convert representations into values, so we introduce new metrics to overcome this shortcoming.

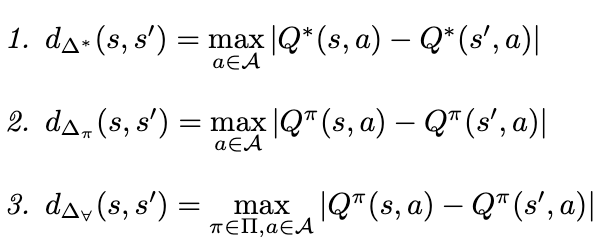
What kind of generalization do these metrics produce when used for value function approximation? We present an empirical evaluation comparing our metrics and showing the importance of the choice of a neighborhood in RL algorithms.

Links

Paper

Poster

Slides

Code