This is a post based on a talk I gave a few times in 2023. I had been meaning to put it in blog post form for over a year but kept putting it off… I guess better late than never. I think some of the ideas still hold, so hope some of you find it useful!

Bigger, better, faster

In the seminal DQN paper, Mnih et al. demonstrated that reinforcement learning, when combined with neural networks as function approximators, could learn to play Atari 2600 games at superhuman levels. The DQN agent learned to do this over 200 million environment frames, which is roughly equivalent to 1000 hours of human gameplay…

This is still quite a lot! We can’t always assume cheap simulators are available; sample efficiency is key!

Kaiser et al. introduced the Atari 100k benchmark which evaluates agents for 100k agent interactions (or 400k environment frames), equivalent to roughly 2 hours of human gameplay.

In Bigger, Better, Faster: Human-level Atari with human-level efficiency, our ICML 2023 paper, we introduced BBF, a model-free agent which was able to achieve superhuman performance with only 100k agent interactions:

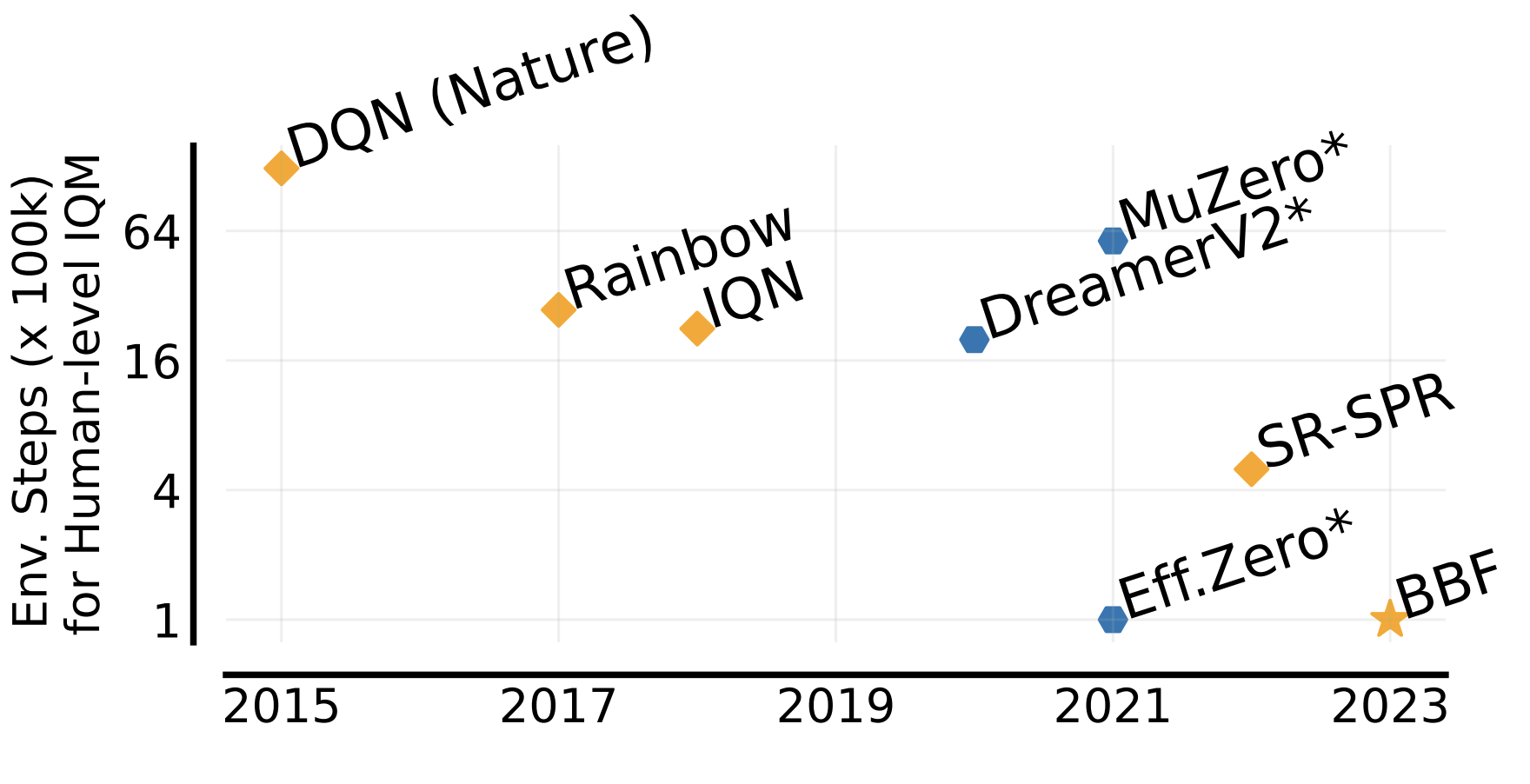
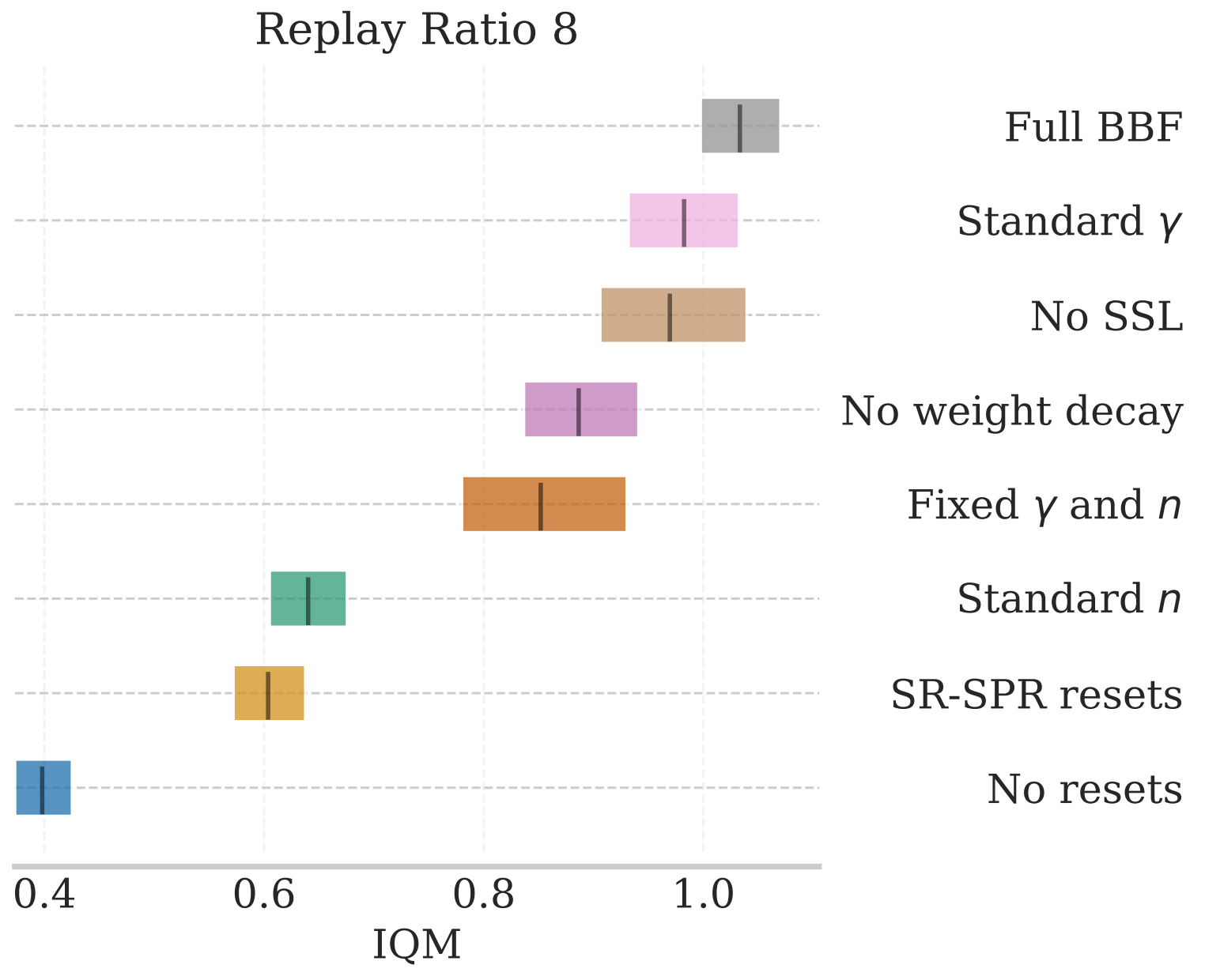
To achieve this, we combined a number of recent techniques from the literature, including SPR and network resets. The following figure ablates each of the components, indicating which proved to be most important.

Yes, but why?

The natural question is: why do we need all these components? We will explore some of the main components in separate sections below.

Self-supervised learning

SPR was the base agent for BBF, which relies on self-supervised learning (BYOL, specifically). What does self-supervised learning buy us?

Good representations!

This is a topic near and dear to me, as I’ve done a lot of work on it, mostly based on bisimulation metrics. To read more about my work in this space, see:

• Scalable methods for computing state similarity in deterministic MDPs
• MICo
• Contrastive Behavioral Similarity Embeddings for Generalization in Reinforcement Learning
• A Kernel Perspective on Behavioural Metrics for Markov Decision Processes
• Metrics and continuity in reinforcement learning

Network resets

Another critical component of BBF is the use of network resets, as used in SR-SPR (and first introduced in The Primacy Bias in Deep Reinforcement Learning). Why do resets help so much?

Mitigate overfitting and maintain plasticity!

There is a growing body of work demonstrating that RL networks tend to overfit to their most recent data, and this seems to cause a loss in plasticity (which is essential for online RL). Some works exploring this idea are:

• The Value-Improvement Path: Towards Better Representations for Reinforcement Learning
• Understanding plasticity in neural networks
• The Dormant Neuron Phenomenon in Deep Reinforcement Learning
• Slow and Steady Wins the Race: Maintaining Plasticity with Hare and Tortoise Networks
• Normalization and effective learning rates in reinforcement learning

Larger networks

The use of larger networks was important to achieve BBF’s ultimate performance; but scaling networks in RL is really hard. More generally, the takeaway is:

Architectures matter!

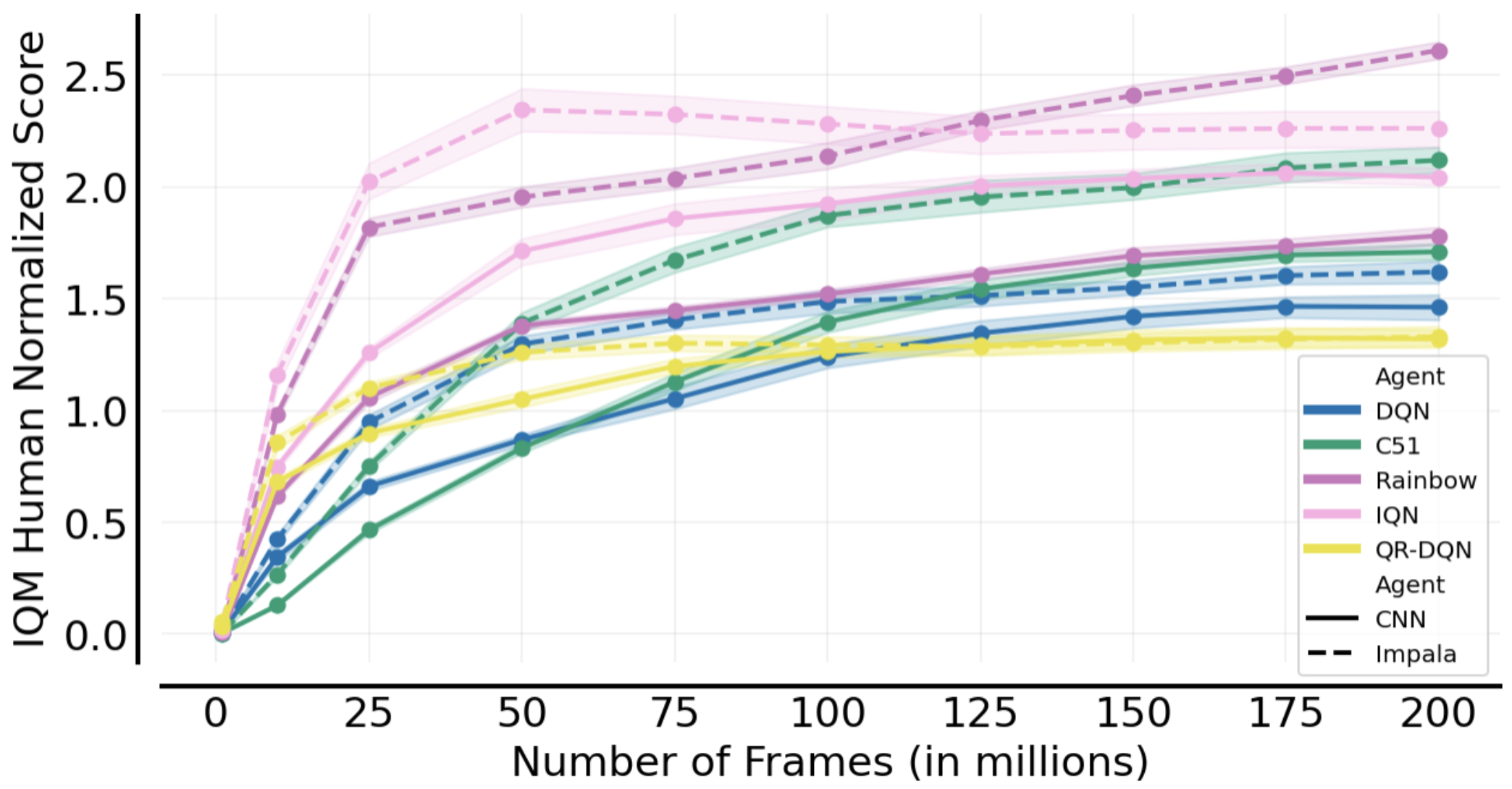
As evidence of this, consider the following plot, evaluating the impact of switching from the original DQN architecture to the IMPALA resnet architecture, and nothing else!

There is a growing body of work exploring alternate architectures for deep RL agents. Here are a few recent ones that I have been involved in.

• The State of Sparse Training in Deep Reinforcement Learning
• In value-based deep reinforcement learning, a pruned network is a good network
• Mixtures of Experts Unlock Parameter Scaling for Deep RL
• Don’t flatten, tokenize! Unlocking the key to SoftMoE’s efficacy in deep RL

The first two, which explore sparse architectures, suggest that we can get away with smaller networks!

Variable horizons

In BBF we used a receding update horizon and an increasing discount factor. Why was this useful?

Bias/variance tradeoff!

When using multi-step returns we make a choice of a value of $n$ in the following equation:

$$Q(x_0, a_0) \leftarrow Q(x_0, a_0) + \alpha \left( \sum_{t=0}^{n}\gamma^t r_t + \max_{a_{n+1}} \gamma^{n+1} Q(x_n, a_{n+1}) - Q(x_0, a_0) \right)$$

As $n$ grows, this approaches a Monte Carlo estimate which has low bias but high variance; if $n = 0$, it is the standard one-step Bellman update which has low variance but high bias. This notion is theoretically explored in “Bias-Variance” Error Bounds for Temporal Difference Updates, where the authors suggest a decreasing schedule for $n$, similar to what we used in BBF.

When using multi-step updates, the choice of the discount factor $\gamma$ affects how much future rewards affect the current state’s value estimate. This isillustrated in the following plot, where the $x$-axis indicates the number of steps in the future the reward is received, and the $y$-axis indicates how much it contributes to the value function for different values of $\gamma$.

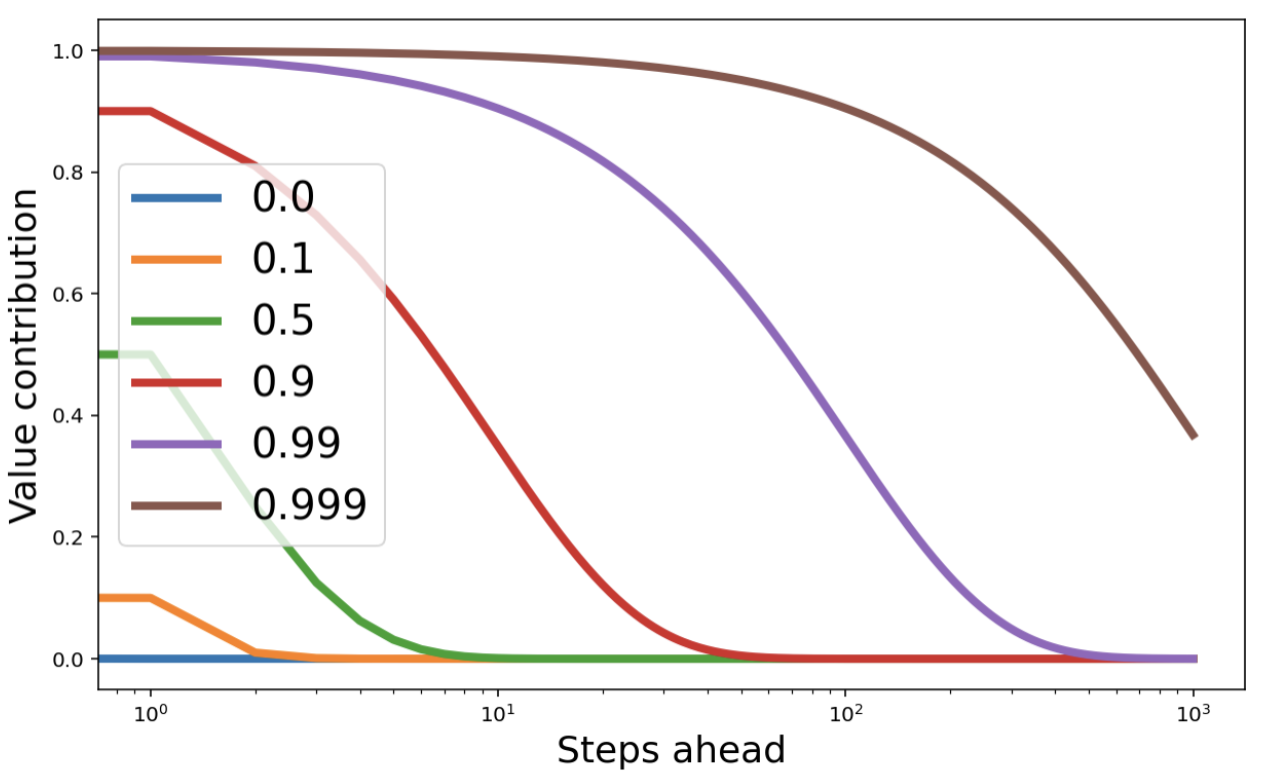
In BBF we use a schedule that increases $\gamma$, inspired by How to Discount Deep Reinforcement Learning: Towards New Dynamic Strategies.

How best to balance this bias-variance tradeoff is still an open problem. We identified the benefits certain types of variance can have in Small batch deep reinforcement learning and in On the consistency of hyper-parameter selection in value-based deep reinforcement learning.

Why does this matter?

The point of this post is not to promote BBF (although I do quite like it). The main takeaway is:

We designed BBF through experimental, not theoretical, RL.

This is by no means discrediting theoretical RL work, as that is very important. However, the reality is that there is still a theory-practice gap in that theoretical results still tell us very little about how modern methods can/should work. We need to approach deep RL as an empirical science. It needs to be empirical because (unfortunately) theoretical results won’t buy us much; and it needs to be scientific in the sense that our aim should be at better understanding how these methods work, as opposed to SotA chasing. I’m very encouraged by recent works (in particular those presented at RLC) that do seem to be pushing in this direction. Let’s continue pushing the frontier of empirical science in RL!

And of course, let’s continue pushing the frontiers of theoretical RL research. I like to make a comparison to physics, where there are theoretical and empirical physicists that are complementary to each other, both aiming at a better understanding of how the universe works.